RL is even more information inefficient than you thought

And implications for RLVR progress

Recently, people have been talking about how it takes way more FLOPs to get a single sample in RL than it does in supervised learning. In pretraining, you get a signal on every single token you train on. In RL, you have to unroll a whole thinking trajectory that’s 10s of 1000s of tokens long in order to get a single reward signal at the end (for example, did the unit test for my code pass/did I get the right answer to this math problem/etc).

But this is only half the problem. Here’s a simple way to compare the learning efficiency of reinforcement learning versus supervised learning:

Bits/FLOP = Samples/Flop * Bits/Sample.

What I haven’t heard people talk about is the other term in our equation: Bits/Sample. And for most of training, the information density per sample is way way lower for RL.

Putting things in plain English

In supervised learning (aka pretraining), you’re just soaking up bits. Every token is a hint at the structure of language, and the mind crafting that language, and the world that mind is seeing. Early in training, when you have a totally random model, you’re just maximally uncertain over all of this content. So each token is just blowing your mind. And you’re getting this exact signal of how wrong you were about the right answer, and what parameters you need to update to be less wrong.

Suppose you start with a randomly initialized model, and you kickstart training. If you’re doing next-token-prediction using supervised learning on “The sky is”, the training loop goes, “It’s actually ‘blue’. You said the probability of ‘blue’ is .001%. Make the connections that were suggesting ‘blue’ way way stronger. Alright, next token.”

In RL with policy gradient, you upweight all the trajectories where you get the answer right, and downweight all the trajectories where you get the answer wrong. But a model that’s not already very smart is just astonishingly unlikely to get the answer right.

If you were doing next-token-prediction on “The sky is” with RL, the training loop would be something like, “Okay, ‘halcyon’ is wrong. Don’t do the thing that led to saying ‘halycon’ … Okay ‘serendipity’ is wrong …” Rinse and repeat this guesswork for somewhere around the number of tokens you have in your vocabulary (on the order of 100,000).

The details

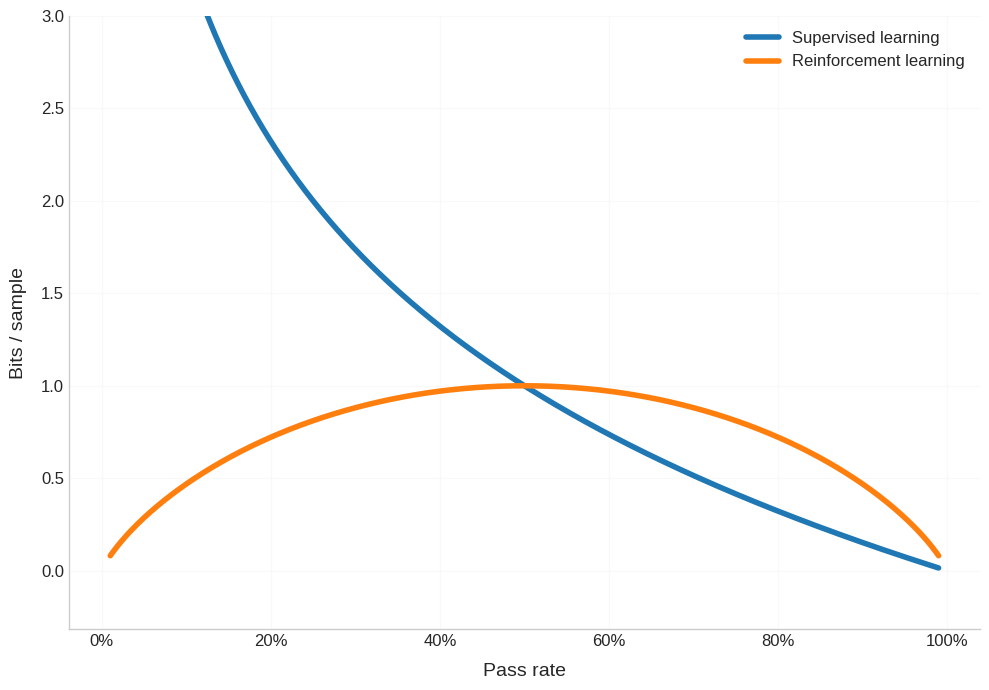
Let’s think about how maximum bits/sample change as the pass rate (p) changes. Pass rate here means how likely you are to say the correct answer. To keep this simple, let’s say the answer is a token long. Then the pass rate when you have a totally untrained model is just 1/ (size of your vocabulary).

In supervised learning, you get told exactly what the right label is for each sample. The amount of new information you learn corresponds to how surprised you are to learn the correct answer - the lower your pass rate (aka prior probability of the correct answer), the more you learned from seeing the correct label. The basic formula for entropy tells us that you can learn -log(p) bits/sample from supervised learning.

In RL, you only get told whether you got the right answer or not. The amount of new information you can extract is bounded by how uncertain you are about this binary outcome. If you almost always pass (p ≈ 1) or almost always fail (p ≈ 0), each trial is very unlikely to surprise you. You’ll learn most when the probability of passing is like a coin toss (p ≈ 0.5). The basic formula for the information content of a binary random variable tells us that you can learn at most Entropy(p) = -p log(p) - (1-p) log(1-p) bits/sample from RL.

Okay let’s plot this.

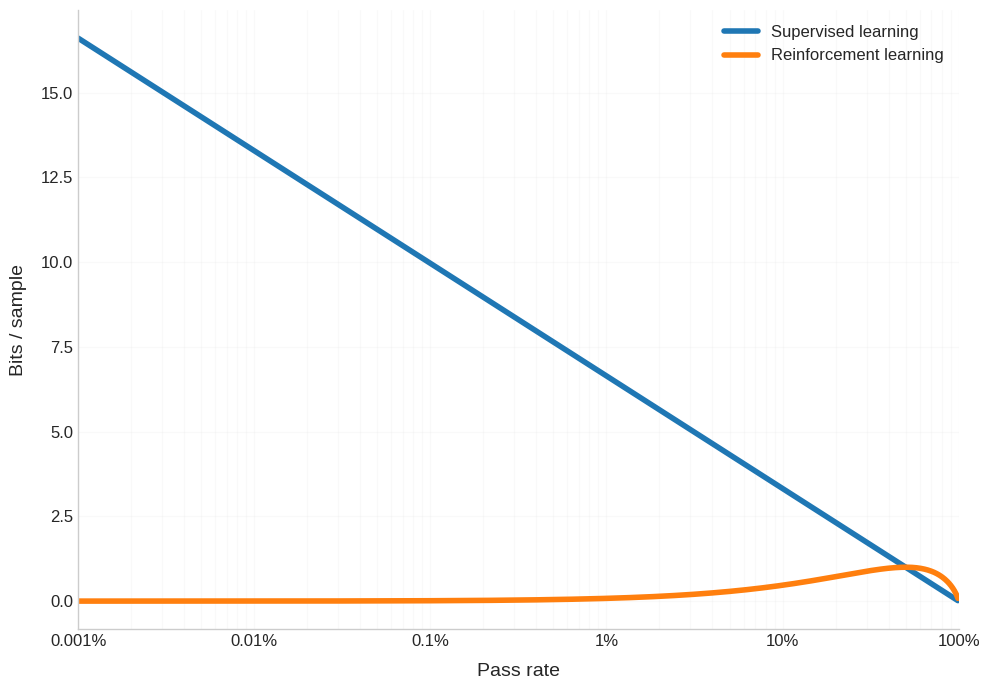
Doesn’t look terrible. Yes, pretraining is much better for half of the pass rate range, but then RL is better for the other half. However, this graph is super misleading. Because what the power law (in scaling laws) implies is that you need an equivalent amount of compute to cross each order of magnitude improvement in the pass rate. If it took you X many FLOPs to go from 1/100,000 pass rate to 1/10,000, then it will take you X many FLOPs to go from 1/10,000 pass rate to 1/1,000. So, we should actually chart the pass rate on a log scale - again, to account for how each increment in the x-axis corresponds to the same number of FLOPs.

Oh boy, is that a sad picture. The regime where RL has comparable information density per sample to pre-training is this tiny slice at the very end of training, when you’ve got a pretty reasonable model anyways.

And again, I want to emphasize that this is totally separate from the point that getting a single sample from RL (aka unrolling a full trajectory before getting any signal) might take upwards of a million times more compute.

It’s actually much worse than this - variance

The situation for RL early in training is actually way worse than what we’ve discussed above. Because you actually have to sample the correct answer in order to learn anything important - it’s not like SL where you get a label for every token, no matter how wrong you are.

And the amount of samples you need to take in order to have a decent shot of actually seeing a correct trajectory increases inversely to your pass rate. If you wanted to do RL on the next token with a totally untrained model, you’d need a batch size of around 300,000 samples in order to have a 95% chance of seeing the correct token at all.

Interestingly, pretraining has the exact inverse problem. There, variance is super high at the END of training. As pretraining progresses, you exhaust more and more of the reducible loss (things your model can actually learn about the data). What remains is mostly the irreducible loss. The irreducible loss is the intrinsic unpredictability of internet text.

How should the prompt, “Bob’s favorite color is” end? Depends on Bob. There’s not some correct answer which your super smart model can actually get good at predicting. But your super smart model is still getting a gradient update on whatever random answer someone put on the internet. And this noise is drowning out the true signal that the couple of actually learnable tokens in the batch are giving you. I don’t know if this is accurate, but it seems like this explosion of variance at the end of pretraining is relevant to why batch sizes are increased as pretraining progresses.

Getting to the Goldilocks zone in RL

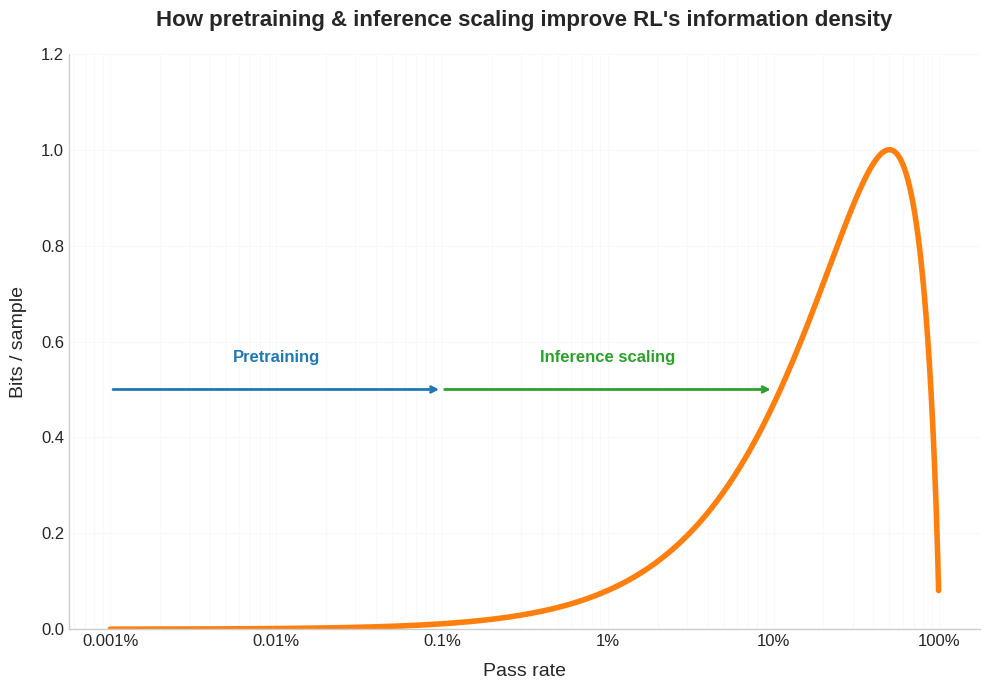
If RL works best in the regime where your pass rate is >>1%, then this raises the question, how can we construct the RL training to get (and keep) models in this learning flow state?

For example, we can think of pretraining AND inference scaling as increasing the pass rate during RL, allowing you to extract far more bits per sample.

It’s been noted that curriculum learning in not especially helpful for pretraining, but often essential for RL. This makes total sense when you think about how RL is only getting meaningful bits per sample in this Goldilocks zone of pass rate, so you really want to order the learning such that the difficulty of challenges increases in tandem with the model’s intelligence.

Our pass rate framework also gives us good intuitions for why self play has been so productive in the history of RL. If you’re competing against a player who is almost as good as you, you are balancing around a 50% pass rate, which is the peak of the bits/sample function in RL.

But self play is not the only way we can imagine of keeping pass rate high through training. Perhaps we can come up with some proxy evaluation which is much more dense. Density here can mean one of two things:

1. Samples/FLOP density: You estimate the final reward using this proxy evaluation, but much earlier on in the episode, saving you the compute of unrolling the full trajectory. This is what a value function does.

2. Bits/Sample density: You come up with a proxy objective which is much easier to pass than the actual test under question. The simplest example I can think of is a process-reward model which says, “Hey, this rollout got the wrong answer, but I can see that its reasoning was on the right track at the start. So let’s up-weight those early tokens.”

Section 4.2 of the Deepseek R1 paper why so far, it’s been hard to develop useful proxy objectives like this for LLMs.

Fewer bits, sure, but very valuable bits

To be fair to RL, while you may be learning far fewer Bits/FLOP in RL, the bits you learn are very important. They are not apples-to-apples comparable to the bits in pretraining. This is for two key reasons:

1. Pre-training is teaching you what the data manifold of the internet looks like, which is only partially and indirectly related to, “How do I perform economically valuable tasks?” Whereas RL has the promise of giving you the good stuff directly.

2. Even if the pre-training corpus contains the instructions about how to accomplish a specific task, it does not have the thinking trace which teaches the model about how to correct its mistakes, or leverage its jagged and non-human repertoire of skills to accomplish the task.

The rebuttal is that those bits are only available for a small fraction of the pass rate range (again, weighted on a log scale to account for how pass rate is trash for most of training).

By the way, now we can understand all these claims about how RLVR is only eliciting the capabilities already latent in the pretrained model. Of course that’s the case. If the pretrained model didn’t have a high enough pass rate to begin with, then RL would have atrocious bits/sample, and thus not be able to learn at all. Move 37 is obviously one famous example where RL did teach a model a de-novo strategy. It’s worth noting that AlphaGo was trained on self play (see above re how self play increases pass rate), and that AlphaGo was surprisingly compute intensive for its time.

The jaggedness of RL

People have pointed out that RLVR is empirically just leading models to associate a thought pattern to a problem type rather than instilling a more general policy of stepping back and thinking through the best approach.

Think about it. How is it possible that we have models which are world-class at coding competitions but at the same time leave extremely foreseeable bugs and technical debt all throughout the codebase?

What explains this weird jaggedness? Here’s an idea I had: RLVR can’t distinguish trajectories that were generated from a more generalizable procedure vs just greedily matching the problem shape to some associated thought process.

When you’re doing policy gradient rollouts, this more complex general policy is extremely unlikely to be ever be sampled, whereas the simple heuristic policy does get sampled and grows in frequency until it reaches fixation. While the general policy recedes further and further from sight.

Then the question is, how do we build a short bridge between simple heuristic solutions and the more complex general solution? And will that bridge just spontaneously emerge as time horizons expand?

My concern is that this general policy of stepping back and making tasteful judgements based on your understanding of the world will continue to be hard to spot-light using RLVR, even on longer time horizon tasks. And so the solution to this jaggedness will require a more general and robust training procedure, not just scaling RLVR.

Human learning

Here we’re only talking about the bits/sample learned from model free RL - aka from some binary outcome at the end of an episode. But of course humans are obviously learning way more efficiently than this. Think about a repeat entrepreneur. We say that she has a ton of hard-won wisdom and experience. Very little of that learning comes from the one bit of outcome from her previous episode (whether the startup succeeded or not).

It’s not clear what the ML analog is for human learning from experience. Clearly, our observations and reflections update our world model (independent of the outcome at the end). And this is playing a very important role in our learning.

Maybe we shouldn’t be asking how we model free RL to ≈50% pass rate, so that can squeeze out a full drop of information from the outcome. Maybe we should be asking, how do humans wring out the buckets of information from the environment?